แรงดันโดยนิยาม คือแรงที่กระทำต่อหนึ่งหน่วยพื้นที่ นั่นคือ

เมื่อ

P คือ แรงดัน หน่วย pascal (pa=N/m²)

F คือ แรง หน่วย newton (N)

A คือ พื้นที่ หน่วย m²

เพื่อให้สามารถทำความเข้าใจแรงดันน้ำได้ดีขี้น พิจารณาถังน้ำตามรูปข้างล่าง

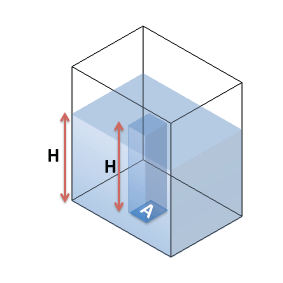
ซึ่งมีน้ำบรรจุสูง H เมตร แรงดันที่ก้นถังจะเป็นเท่าไหร่

จากสมการแรงดัน เราต้องหาว่าแรงกดของน้ำที่กันถังต่อหน่วยพื้นที่ก้นถังคือเท่าไหร่

วิธีคิดวิธีหนึ่งคือให้เรามองที่พื้นที่ A ที่ก้นถัง จะเห็นว่าปริมาตรน้ำที่อยู่เหนือพื้นที่ A เป็น H×A ดังนั้น เราจะสามารถคำนวณแรงดันที่ก้นถังได้จากน้ำหนักของน้ำปริมาตร H×A ดังนี้

เมื่อ

m คือ มวลของน้ำ หน่วย Kg

g คือ อัตราเร่งเนื่องจากแรงโน้มถ่วงของโลก เป็นค่าคงที่ ที่ประมาณ 9.81 m/s²

ρ คือ ความหนาแน่นของน้ำ หน่วย Kg/m³ มีค่าประมาณ 1,000 Kg/m³ ที่น้ำ 4°C (ค่า ρ ของน้ำนี้ จะขี้นกับอุณหภูมิของน้ำ ไดยจะไล่จาก 1,000 Kg/m³ ที่น้ำ 4°C ลงไป ถีง 992 Kg/m³ ที่น้ำ 40°C (ดูค่า ρ ของน้ำที่อุณหภูมิต่างๆได้ที่ตารางล่างสุดในหน้าเวปนี้) จึงถือว่าค่าค่อนข้างคงที่ในช่วงอุณหภูมิน้ำที่ใช้งานทั่วไปในระบบจ่ายน้ำทางการเกษตร)

H คือ ความสูงของน้ำ หน่วยเป็นเมตร (m)

จะเห็นได้ว่าแรงดันของน้ำที่ก้นถังจะขี้นกับความสูงของน้ำในถังเท่านั้น (ถ้าไม่มีการเปลี่ยนแปลงอุณหภูมิของน้ำ)

ดังนั้น จึงมีการนำความสูงของน้ำมาใช้เป็นหน่วยของแรงดันน้ำเช่นกัน โดยเรียกเป็น Head มีหน่วยเป็น เมตรของน้ำ ยกตัวอย่างเช่น ถ้าเรามีถังน้ำบรรจุน้ำสูง 8 เมตร แรงดันของน้ำที่พร้อมให้เรานำมาใช้งาน หากเราเจาะรูที่ก้นถังจะเป็น Head = 8 เมตรของน้ำ ทั้งนี้ เราสามารถหาความสัมพันธ์ระหว่างหน่วย Head (m) กับ Pascal ได้จากสมการด้านบนดังนี้คือ

นอกจากนี้ อีกหนึ่งหน่วยของแรงดันที่ควรรู้จัก เพราะมีการใช้งานที่แพร่หลาย คือ หน่วย bar โดยมีความสัมพันธ์กับหน่วย pascal ดังนี้

สิ่งที่เราควรจดจำได้ในการออกแบบระบบน้ำทั่วไปคือ Head น้ำหนึ่งเมตร เท่ากับประมาณ กี่ bar

ถ้าเราลองคำนวณที่ น้ำ 20°C ซึ่งมีความหนาแน่น 998.2 Kg/m³ เราจะได้ แรงดันของ Head 1 เมตร เป็น

นั่นคือ Head 1 m ของน้ำ (20°C) จะเทียบเท่ากับแรงดันประมาณ 0.098 bar หรือ ประมาณคร่าวๆ ได้ เป็น 0.1 bar

โดยทั่วไป วิธีคิดง่ายๆก็คือ

• Head น้ำ 1 เมตร จะเทียบเท่ากับแรงดันประมาณ 0.1 bar
• Head น้ำ 10 เมตร จะเทียบเท่ากับแรงดันประมาณ 1 bar

การคำนวณจะแยกเป็น 2 กรณี คือ กรณีที่ในระบบไม่มีแรงเสียดทาน และในกรณีที่ระบบมีแรงเสียดทาน

การคำนวณแรงดันของน้ำจากจุดหนึ่งไปอีกจุดหนึ่งในระบบที่ไม่มีแรงเสียดทาน

ในที่นี้เราจะพิจารณาระบบน้ำระบบหนึ่ง ตามสมมติฐานด้างล่างนี้

• 1. น้ำเป็นเนื้อเดียวกันทั้งหมด (นั่นคือน้ำทุกจุดในระบบต่อเนื่องถึงกันหมด)
• 2. น้ำไม่สามารถถูกบีบให้เล็กลงได้ (incompressible liquid)
• 3. ไม่มีแรงเสียดทานต่อการไหลของน้ำในระบบ

ในกรณีนี้หากเราทราบแรงดันของน้ำ ณ. จุดหนึ่ง เราจะสามารถหาแรงดันของน้ำ ณ. อีกจุดหนี่งได้จาก Bernoulli Equation

เมื่อ

υ คือ อัตราเร็วของการไหลของน้ำ (m/s)

Z คือ ความสูงของน้ำเทียบกับจุดอ้างอิง (m)

โดยเราสามารถเขียนสมการนี้ในรูปของ Head ได้้เป็น

จะเห็นได้ว่า ในการใช้สมการดังกล่าว เราต้องทราบอัตราเร็วในการไหลของน้ำ ซึ่งจะสามารถคำนวณได้จากอัตราไหลของน้ำและพื้นที่หน้าตัดของน้ำ ณ. จุดที่สนใจ ทั้งนี้เราจะคำนวณจากกรณีที่ทั่วไปที่สุด คือการไหลของน้ำเต็มท่อสายส่ง ที่มีอัตราไหลของน้ำ Q (m³/s) และพื้นที่หน้าตัดของท่อ A (m²) ซึ่งจะได้ว่า

ตัวอย่างที่ 1: การคำนวณแรงดันของน้ำในระบบไร้แรงเสียดทาน

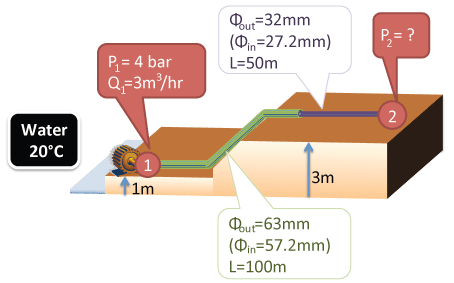
คำนวณหาแรงดัน ณ.จุดที่ 2

ในที่นี้จะใช้ สมการ Bernoulli ในรูปของ Head ดังนี้

$${\upsilon_1^2 \over 2 g} + H_1 + Z_1 = {\upsilon_2^2 \over 2 g} + H_2 + Z_2$$ $$H_2 = {\upsilon_1^2 - \upsilon_2^2 \over 2 g} + H_1 + Z_1 - Z_2$$

สำหรับ น้ำ 20°C จะสามารถคำนวณ Head ณ. จุดที่ 1 ได้เป็น

$$H_1={4 \over 0.098}= 40.8 m$$

คำนวณหาอัตราเร็วของน้ำ ณ. จุดที่ 1 ได้ดังนี้

$$\upsilon_1 = {Q_1 \over A_1} ={Q_1 \over π{\left(D_1 \over 2 \right)}^2}={\frac{3}{3600} \over π \left({\frac{57.2}{1000} \over 2} \right)^2} = 0.324 \frac{m}{s}$$

เนื่องจากไม่มีการสูญเสียน้ำไปที่อื่นระหว่างจุดที่ 1 และจุดที่ 2 อัตราไหลของน้ำ ณ. จุดที่ 2 จะต้องเท่ากันกับ ณ. จุดที่ 1 เพราะฉะนั้น เราจะสามารถคำนวณหาอัตราเร็วของน้ำ ณ. จุดที่ 2 ได้ดังนี้

$$\upsilon_2 = {Q_2 \over A_2} ={Q_2 \over π{\left(D_2 \over 2 \right)}^2}={\frac{3}{3600} \over π \left({\frac{27.2}{1000} \over 2} \right)^2} = 1.434 \frac{m}{s}$$

และจะสามารถคำนวณหา Head ณ.จุดที่ 2 ได้จาก

$$H_2 = {0.324^2 - 1.434^2 \over 2 \times 9.81} + 40.8 + 1- 3$$ $$= 38.7 m$$

หรือคิดเป็น bar จะได้

$$P_2= 38.7 \times 0.098 = 3.79 bar$$

การคำนวณแรงดันของน้ำจากจุดหนึ่งไปอีกจุดหนึ่งโดยคำนึงถึงแรงเสียดทาน

โดยทั่วไปแล้วนั้น การไหลของน้ำในท่อจะก่อให้เกิดแรงเสียดทานในระดับที่ต้องนำมาพิจารณาด้วย โดยยิ่งถ้าผิวท่อด้านในมีความหยาบมาก แรงเสียดทานจะยิ่งมากขี้น และในขณะเดียวกัน ถ้าน้ำในท่อมีอัตราเร็วมากขี้น ผลจากแรงเสียดทานก็จะเพิ่มมากขี้นด้วย

ในการคำนวณแรงดัน ณ. จุดหนึ่งไปยังอีกจุดหนึ่งในระบบ เรายังคงสามารถใช้สมการ Bernoulli ในหัวข้อที่แล้วได้ แต่จำเป็นต้องมีการนำการสูญเสียแรงดัน Head loss (หรือการสูญเสียพลังงาน) ที่เกิดจากแรงเสียดทานรวมเข้าด้วย

โดยถ้าแรงดันสูญเสียจากการไหลจากจุดที่ 1 ไป จุดที่ 2 ในรูป Head loss คือ ΔH₁₂ เราจะสามารถเขียนเป็นสมการได้ดังนี้

แรงดันสูญเสียในระบบน้ำโดยหลักๆแล้ว ประกอบด้วย

• A. แรงดันสูญเสียที่เกิดจากการไหลในท่อ
• B. แรงดันสูญเสียที่เกิดจากการไหลผ่าน fittings, valves หรืออุปกรณ์ต่างๆ

A. การคำนวณ Head loss ที่เกิดจากการไหลในท่อ

สำหรับท่อที่มีคุณสมบัติไม่เปลี่ยนแปลงตามตำแหน่งตามยาวของท่อ Head loss จะแปรผันตรงกับความยาวของท่อที่น้ำต้องไหลผ่าน ตามสมการ

โดย

ΔH_Q,pipe คือ Head loss จากการไหลจากจุดที่ 1 ไป จุดที่ 2

J_Q,pipe คือ การสูญเสียพลังงาน (ไม่มีหน่วย) ซึ่งจะเป็นค่าเฉพาะตัวของท่อนั้นๆ ที่อัตราไหลหนึ่งๆ

L₁₂ คือ ความยาวของท่อจากจุดที่ 1 ไป จุดที่ 2

จุดสำคัญในการคำนวณหา Head loss ที่เกิดจากการไหลของท่อ จึงเป็นการหา J_Q,pipe ของท่อนี้ให้ได้ ซึ่งจะเป็นหัวข้อหลักที่จะกล่าวถึงต่อไปนี้

การหาค่าของ J_Q,pipe

มี 2 วิธีหลักๆ คือ 1. ดูจากแผนภูมิ และ 2. คำนวณจากสมการ

1. หาค่า J_Q,pipe จากแผนภูมิ

ในที่นี้ ได้แสดงตัวอย่างของแผนภูมิ เป็นสามตัวอย่าง ดังนี้

แผนภูมิ J_Q,pipe ตัวอย่าง A*

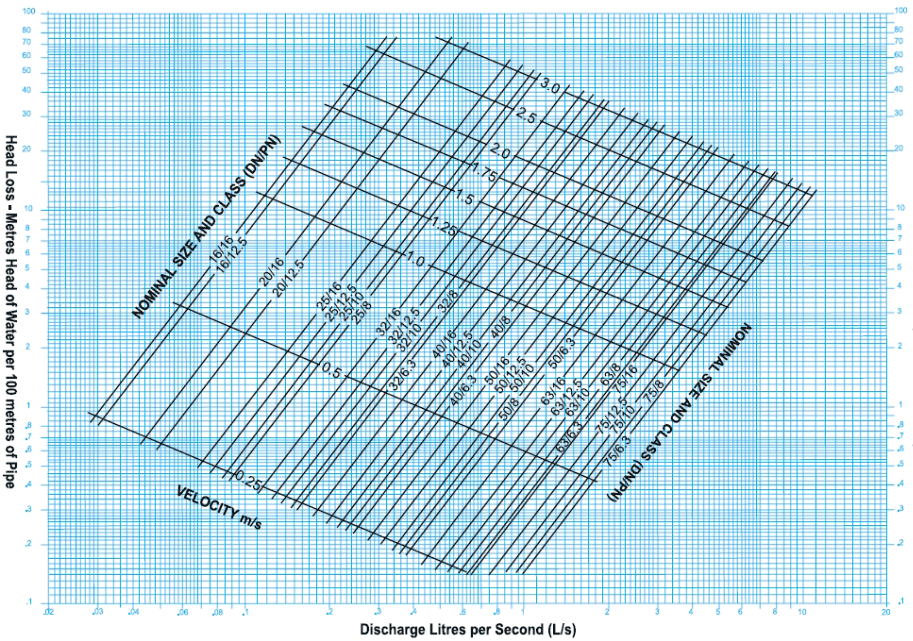
*Source: http://www.vinidex.com.au/technical/pe-pressure-pipe/hydraulic-design-for-pe-pipes/

แผนภูมิ J_Q,pipe ตัวอย่าง B**

**Orignial document: --LINK--

แผนภูมิ J_Q,pipe ตัวอย่าง C***

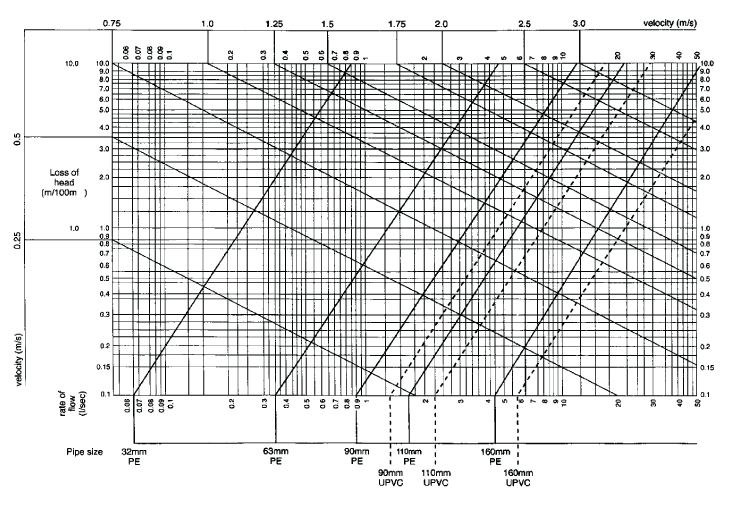
***Source: http://helid.digicollection.org/fr/d/Js2974e/6.12.html แต่มีการแก้ไขหน่วย m/100mm ของแกน y ให้เป็น 1/100m ในหน้าเวปนี้

ในบางครั้งผู้ผลิตอาจระบุ J_Q,pipe ในรูปของแรงดันสูญเสีย/ความยาวในหน่วยอื่นๆ ซึ่งเราก็สามารถแปลงเป็น J_Q,pipe ในรูปที่ไม่มีหน่วยได้ โดยเปลี่ยนแรงดันให้อยู่ในรูป Head (m) ก่อน

ในบางกรณี ทางผู้ผลิตอาจมิได้มีข้อมูล J_Q,pipeให้ จึงอาจจำเป็นต้องหาแผนภูมิที่ทราบว่ามีการใช้วัสดุและวิธีการผลิตที่ใกล้เคียงกัน หรืออาจคำนวณเองจากสมการตามหัวข้อต่อไป

2. หาค่า J_Q,pipe โดยใช้สมการ

สมการที่ใช้ในการคำนวณ J_Q,pipe มี 2 สมการหลักๆ คือสมการ Hazen-Williams และ สมการ Darcy-Weisbach

• 2.1 สูตรของ Hazen-Williams

สมการของ Hazen-Williams เป็นสูตร empirical ซึ่งจะคำนวณได้ง่ายกว่าสมการของ Darcy-Weisbach แต่มีข้อกำหนดในการใช้ คือ ท่อควรมีเส้นผ่านศูนย์กลางภายในมากกว่า 3 นิ้ว และมีอัตราไหลไม่ต่ำกว่า 11.3 m³/hr (50 gpm)

สมการของ Hazen-Williams เขียนได้ดังนี้

$$J_{Q,pipe} = 10.23 \left( \frac {Q} {C} \right)^{1.85} D^{-4.8655} $$

โดย

Q คือ อัตราไหล (m³/s)

C คือ roughness coefficient (ไม่มีหน่วย)

D คือ เส้นผ่านศูนย์กลางภายในของท่อ (m)

ค่าของ C ของวัสดุท่อชนิดต่างๆ มีดังนี้ (ข้อมูลจาก The Engineering ToolBox:--LINK--)

ตารางแสดงค่า Hazen-Williams Coefficient (C)

Material	Hazen-Williams Coefficient (C)
ABS - Acrylonite Butadiene Styrene	130
Aluminum	130 - 150
Asbestos Cement	140
Asphalt Lining	130 - 140
Brass	130 - 140
Brick sewer	90 - 100
Cast-Iron - new unlined (CIP)	130
Cast-Iron 10 years old	107 - 113
Cast-Iron 20 years old	89 - 100
Cast-Iron 30 years old	75 - 90
Cast-Iron 40 years old	64-83
Cast-Iron, asphalt coated	100
Cast-Iron, cement lined	140
Cast-Iron, bituminous lined	140
Cast-Iron, sea-coated	120
Cast-Iron, wrought plain	100
Cement lining	130 - 140
Concrete	100 - 140
Concrete lined, steel forms	140
Concrete lined, wooden forms	120
Concrete, old	100 - 110
Copper	130 - 140
Corrugated Metal	60
Ductile Iron Pipe (DIP)	140
Ductile Iron, cement lined	120
Fiber	140
Fiber Glass Pipe - FRP	150
Galvanized iron	120
Glass	130
Lead	130 - 140
Metal Pipes - Very to extremely smooth	130 - 140
Plastic	130 - 150
Polyethylene, PE, PEH	140
Polyvinyl chloride, PVC, CPVC	150
Smooth Pipes	140
Steel new unlined	140 - 150
Steel, corrugated	60
Steel, welded and seamless	100
Steel, interior riveted, no projecting rivets	110
Steel, projecting girth and horizontal rivets	100
Steel, vitrified, spiral-riveted	90 - 110
Steel, welded and seamless	100
Tin	130
Vitrified Clay	110
Wrought iron, plain	100
Wooden or Masonry Pipe - Smooth	120
Wood Stave	110 - 120

*อย่างไรก็ดี ควรมีความระมัดระวังในการเลือกใช้ค่า C เพราะ คุณสมบัติของท่อ ขี้นอยู่ไม่น้อยกับคุณภาพในการผลิต

• 2.2 สูตรของ Darcy-Weisbach

เป็นสมการดังนี้

$$J_{Q,pipe} = {8 f Q^2 \over \pi^2 D^5 g}$$

โดย

Q คือ อัตราไหล (m³/s)

f คือ Darcy friction factor (ไม่มีหน่วย)

D คือ เส้นผ่านศูนย์กลางภายในของท่อ (m)

g คือ อัตราเร่งเนื่องจากแรงโน้มถ่วงของโลก

ข้อสำคัญในการใช้สมการ Darcy-Weisbach คือ ต้องทราบค่า Darcy friction factor (f) ก่อน ซึ่งวิธีการหา f นี้ จะมี 2 วิธีหลัก คือใช้แผนภูมิ หรือใช้สมการ แต่ไม่ว่าจะเป็นวิธีใด เราจำเป็นต้องทราบ Reynolds number (Re) ซึ่งเป็นค่าที่บ่งบอกลักษณะการไหลของของเหลวเสียก่อน

ตัวเลข Reynolds คำนวณได้จากสมการ

$$Re={\rho \upsilon D \over \mu} $$

โดย

Re คือ Reynolds number (ไม่มีหน่วย)

ρ คือ ความหนาแน่นของน้ำ (Kg/m³)

υ คือ อัตราเร็วของการไหลของน้ำ (m/s)

D คือ เส้นผ่านศูนย์กลางภายในของท่อ (m)

μ คือ ความหนืดเชิงไดนามิค dynamic visocity (Pa·s)

ความหนืดเชิงไดนามิคของน้ำที่อุณหภูมิต่างๆ สามารถดูได้ที่ตารางล่างสุดในหน้าเวปนี้

เมื่อคำนวณ ค่า Reynolds numberได้แล้ว จะสามารถทราบลักษณะการไหลของน้ำในท่อได้ ดังนี้

ตารางแสดงรูปแบบการไหลที่ค่า Reynolds number ต่างๆ

Re≤2,100	Laminar Flow
2,100<Re<4,000	Transition Flow
Re≥4,000	Turbulence Flow

หลังจากทราบค่า Reynolds number เราจะหาค่า Darcy friction factor ได้ดังนี้

• 2.2.1 การหา Darcy friction factor จาก Moody Diagram

พิจารณา Moody Diagram ข้างล่างนี้



แผนภูมิ Moody****



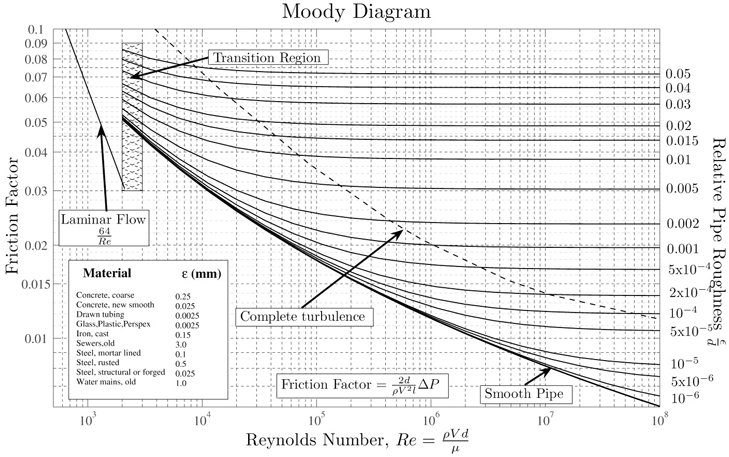
****source=http://en.wikipedia.org/wiki/Moody_chart

จะเห็นได้ว่า เราจำเป็นต้องทราบความหยาบของผิววัสดุด้านในของท่อ คือ ε (m) แล้วนำไปหารด้วยขนาดเส้นผ่านศูนย์กลางภายในของท่อ D (m) เพื่อให้ได้ ความหยาบเชิงอ้างอิง (relative roughness) ก่อน เพื่อนำไปอ่านค่าในแผนภูมิต่อไป

โดยหากไม่ทราบความหยาบภายในของท่อ ก็สามารถอ้างอิงได้จาก ที่นี่ แต่ก็ควรมีความระมัดระวังในการใช้ เพราะคุณสมบัติของท่อขี้นอยู่ไม่น้อยกับคุณภาพการผลิต

ข้อสังเกต หากการไหลยังเป็น laminar ความหยาบภายในของผิวท่อจะไม่มีผลต่อค่า friction factor แต่อย่างใด

• 2.2.2 การหา Darcy friction factor จากสมการ

ในกรณีนี้ สมการที่ใช้จะขี้นอยู่กับว่า การไหลเป็นแบบใด ดังนี้

• 2.2.2.1 การไหลแบบ laminar (Re≤2,100)

ในกรณีนี้ Darcy friction factor จะคำนวณ ได้จาก

$$f = \frac{64}{Re} $$

ซึ่งจะไม่ขี้นกับความหยาบภายในของผิววัสดุด้านในของท่อ

• 2.2.2.2 การไหลในช่วง Transition (2,100<Re<4,000)

เนื่องจากการไหลในช่วงนี้ คาดคะเนได้ยาก จีงไม่สามารถกำหนดตายตัวได้ว่าควรจะใช้สมการใด อย่างไรก็ดี สำหรับการออกแบบ แนะนำให้ใช้สมการของช่วง Turbulence จะปลอดภัยกว่า

• 2.2.2.3 การไหลแบบ Turbulence (Re≥4,000)

สูตรที่ใช้ในการคำนวณหา Darcy friction factor ในกรณีนี้ คือสมการ Colebrook–White

$$ \frac{1}{\sqrt f}=-2 log \left(\frac{\epsilon}{3.7D} + \frac{2.51}{Re \sqrt f} \right)$$

โดย

f คือ Darcy friction factor (ไม่มีหน่วย)

Re คือ Reynolds number (ไม่มีหน่วย)

ε คือ ความหยาบของผิววัสดุด้านในของท่อ (m)

D คือ เส้นผ่านศูนย์กลางภายในของท่อ (m)

จะเห็นได้ว่าสมการข้างต้นนี้ จะไม่สามารถคำนวณออกได้โดยตรงโดยที่ไม่ใช้ iteration ดังนั้น ในที่นี้ จะแนะนำให้ใช้สมการที่เป็นการประมาณ แต่มีความแม่นยำสูงโดยไม่จำเป็นต้องใช้ iteration ทั้งนี้ จะมีสมการหลายชุดด้วยกันที่สามารถใช้ประมาณได้ แต่ในที่นี้จะแนะนำเพียงสมการของ Goudar-Sonnad ซึ่งเป็นกลุ่มสมการข้างล่างนี้

$$a=\frac{2}{ln(10)}$$ $$b=\frac{\epsilon \over D}{3.7}$$ $$d=\frac{ln(10) Re}{5.02}$$ $$s=bd+ln(d)$$ $$q=s^{\frac {s} {s+1}}$$ $$g=bd+ln \frac{d}{q}$$ $$z=ln \frac {q} {g}$$ $$D_{LA}=z \frac {g} {g+1}$$ $$D_{CFA}=D_{LA} \left( 1+\frac{z \over 2} {(g+1)^2 + {z \over 3} (2 g - 1)}\right)$$ $$f=\left[ a \left( ln \frac{d}{q} + D_{CFA} \right)\right] ^ {-2}$$

โดย

f คือ Darcy friction factor (ไม่มีหน่วย)

Re คือ Reynolds number (ไม่มีหน่วย)

ε คือ ความหยาบของผิววัสดุด้านในของท่อ (m)

D คือ เส้นผ่านศูนย์กลางภายในของท่อ (m)

เนื่องจากขั้นตอนในการคำนวณ Head loss ของท่อค่อนข้างจะมีหลายวิธี จึงขอสรุปเป็นแผนภูมิ เพื่อให้เข้าใจขั้นตอนได้ง่ายขึ้น ดังนี้

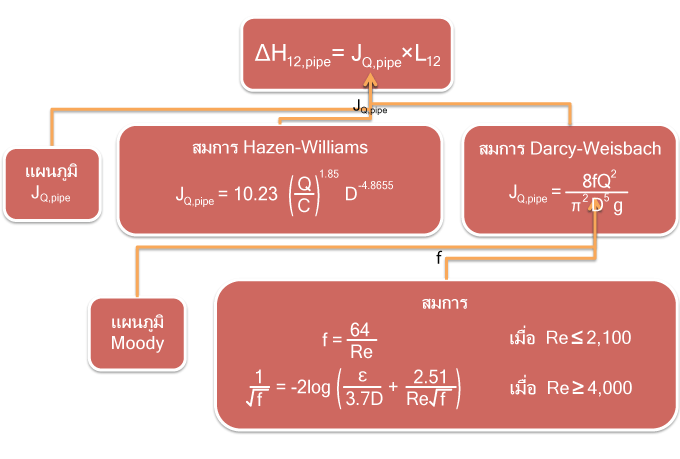
B. แรงดันสูญเสียที่เกิดจากการไหลผ่าน fittings, valves หรืออุปกรณ์ต่างๆ

การคำนวณ Head loss ที่เกิดจากการไหลผ่าน fittings, valves หรืออุปกรณ์ต่างๆ โดยทั่วไป สามารถคำนวณหาได้จาก

โดย

ΔH_local คือ Head loss ที่เกิดจากการไหลผ่านอุปกรณ์หนึ่งๆ (m)

K คือ ค่าคุณสมบัติของการสูญเสียแรงดันของอุปกรณ์นั้นๆ (ไม่มีหน่วย)

υ คือ ความอัตราเร็วของการไหลของน้ำ (m/s)

ทั้งนี้ ค่า K อาจสามารถทราบได้จากการสอบถามทางผู้ผลิต หรือจากการทำการทดสอบเอง

C. การคำนวณ Head loss รวม

เมื่อทราบ Head loss จากจุดต่างๆที่น้ำไหลผ่านแล้ว เราจะสามารถคำนวณหา Head loss รวมที่เกิดจากการไหลจากจุดที่ 1 ไปจุดที่ 2 ได้ โดยเพียงนำ Headloss ทั้งหมดมาบวกรวมกัน

เมื่อเราทราบแรงดันที่หัวจ่าย เราจะสามารถคำนวณอัตราจ่ายน้ำของหัวจ่ายได้ตามสมการ

โดย

Q_d คืออัตราไหลของน้ำที่หัวจ่าย (m³/s)

K_d คือ ค่าคงที่ของการจ่ายน้ำของอุปกรณ์นั้นๆ

x คือ ค่าคงที่ exponent ของการจ่ายน้ำของอุปกรณ์นั้นๆ ไม่มีหน่วย มีค่า 0 ถึง 1

H_d คือ Head ณ. หัวจ่าย (m)

ทั้งนี้ ค่า K_d และ x เป็นค่าคุณสมบัติของหัวจ่าย ซึ่งเป็นข้อมูลที่ทราบได้จากทางผู้ผลิต หรือจากการทำการทดสอบเอง

จากสมการ จะเห็นได้ว่า x เป็นค่าสำคัญที่จะบ่งบอกว่าอัตราไหลของหัวจ่ายนั้นๆ ขึ้นกับการเปลี่ยนแปลงของแรงดันที่หัวจ่ายมากน้อยเพียงใด ถ้า x เข้าใกล้ 0 แสดงว่าหัวจ่ายนั้นมีความเสถียรในปริมาณน้ำที่จ่ายในภาวะที่แรงดันที่หัวจ่ายเปลี่ยนแปลง ในทางตรงกันข้าม ถ้า x เข้าใกล้ 1 แสดงว่าหัวจ่ายนั้นมีอัตราจ่ายน้ำแปรผันตรงกับแรงดันที่หัวจ่าย โดย ค่า x ของ หัวฉีด (nozzle) ทั่วไป เช่น สปริงเกลอร์ (sprinkler) จะมีค่าอยู่ที่ประมาณ 0.5

ในหลายครั้ง การต่อระบบน้ำมักจะต้องเกี่ยวข้องกับการต่อหัวจ่ายชนิดเดียวกันมากกว่าหนี่งหัว ณ. จุดต่างๆในระบบ และมักต้องการให้มีอัตราจ่ายน้ำของแต่ละหัวจ่ายใกล้เคียงกันเพื่อความทั่วถึงในการรดน้ำในบริเวณกว้าง ซึ่งในกรณีนี้ เราจะลองเปรียบเทียบการจ่ายน้ำของหัวจ่ายน้ำชนิดหนึ่ง ที่แรงดัน H₁ และ H₂ โดยใช้สมการด้านบน ซึ่งจะได้ว่า

ดังที่ได้กล่าวข้างต้น ในกรณีของสปริงเกลอร์ทั่วไป ค่า x จะอยู่ที่ประมาณ 0.5 นั่นคือ

ดังนั้น หากเราต้องการให้อัตราไหลของแต่ละหัวจ่ายต่างกันที่ ไม่เกิน 10% โดยยกตัวอย่างเช่นในกรณีที่ Q_d,2 เป็น 90% ของ Q_d,1 พอดี จะได้ว่า

ซึ่งจะเห็นได้ว่า ถ้าเราต้องการให้อัตราไหลของหัวจ่าย ณ. จุดที่ 1 และ จุดที่ 2 ต่างกันไม่เกิน 10% เราต้องควบคุมแรงดันที่หัวจ่ายให้ต่างกันประมาณไม่เกิน 20% และนี่เป็นที่มาของหลักการในการออกแบบระบบน้ำที่ใช้กันทั่วไป ที่จะพยายามออกแบบระบบให้หัวจ่ายแต่ละตัวในระบบ เห็นแรงดันต่างกันประมาณไม่เกิน 20% อย่างไรก็ดี ในกระบวนการผลิตหัวจ่าย อาจไม่สามารถควบคุมให้ K_d ของหัวจ่ายทุกตัวเท่ากันได้ ดังนั้น ในการออกแบบระบบน้ำ จึงอาจต้องควบคุมให้แรงดันต่างของแต่ละหัวจ่ายต่ำกว่า 20% บ้าง

ในการออกแบบระบบน้ำ หลายครั้งเช่นกันที่จะมีการใช้ท่อที่มีหัวจ่ายแบบเดียวกัน ติดตั้งที่ระยะห่างเท่าๆกันตามแนวยาวของท่อ (ระบบ manifold) ดังแสดงในรูปข้างล่างนี้

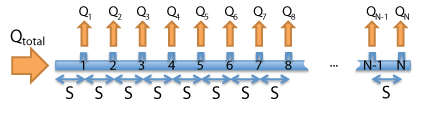
ลักษณะที่ควรทราบของระบบ manifold ดังกล่าว มีดังนี้

• อัตราไหลจากต้นท่อไปจนถึงปลายท่อจะลดลงเรื่อยๆ (เพราะน้ำค่อยๆถูกจ่ายไปแต่ละหัวจ่าย)
• Head loss ต่อความยาวท่อจะลดลงเรื่อยๆเพราะอัตราไหลในท่อค่อยๆลดลง
• หากหัวจ่ายมีลักษณะการจ่ายน้ำแบบหัวฉีดหรือสปริงเกลอร์ จะพบว่า
  • แรงดันของแต่ละหัวจ่าย จะลดลงในช่วง 40% แรกของความยาวท่อ เร็วกว่าในช่วง 60% ที่เหลือ
  • อัตราไหลของแต่ละหัวจ่าย จะลดลงในช่วง 40% แรกของความยาวท่อ เร็วกว่าในช่วง 60% ที่เหลือ
  • หัวจ่ายที่มีแรงดันและอัตราไหลเป็นค่าเฉลี่ยของทั้งสายจะอยู่ที่ระยะประมาณ 40% ของความยาวสายนับจากต้นทาง
  • 3/4 ของ Head loss ในสายจะเกิดอยู่ที่ประมาณ 40% แรกของความยาวสาย

วิธีการคำนวณ Head loss ในระบบ manifold

เราสามารถคำนวณได้จากสมการข้างล่างนี้คือ

โดย

ΔH_12,manifold คือ Head loss จากต้นถึงปลาย manifold (m)

F คือ ค่าตัวคูณลดของระบบ manifold เทียบกับ ถ้าน้ำทั้งหมดไหลจากต้นทางไปออกที่ปลายทางโดยไม่มีจุดจ่ายระหว่างทาง

ΔH_12,pipe คือ Head loss จากต้นถึงปลายท่อ (m) โดยคิดว่าน้ำทั้งหมดที่ส่งเข้าสาย (Q_total) ไหลผ่านท่อทั้งหมด (ราวกับไม่มีหัวจ่ายระหว่างทาง)

โดยสามารถคำนวณ F ได้จากสมการ^†

เมื่อ

m คือค่าคงที่ที่ขึ้นกับลักษณะของหัวจ่าย โดยปกติจะใช้ที่ค่า 1.85, 1.9, หรือ 2.0

N คือจำนวนหัวจ่าย

สำหรับระบบสปริงเกลอร์ ทั่วไป สามารถใช้ m=2 ได้ และทั้งนี้ สมการดังกล่าวคำนวณโดยคิดว่าจุดจ่ายจุดแรกห่างจากทางเข้า manifold เท่ากับระยะห่างระหว่างหัวจ่าย (S) ตามรูปภาพที่แสดงข้างต้น

การออกแบบระบบน้ำจะเกี่ยวข้องกับการเลือกและวางตำแหน่งอุปกรณ์ระบบน้ำต่างๆเช่น ปัมป์ หัวจ่ายน้ำ fittings valves และอุปกรณ์อื่นๆ รวมถึงการเลือกสเปคและขนาดของท่อส่งน้ำที่เหมาะสม โดยในการเลือกและวางตำแหน่งหัวจ่าย ควรปรึกษาทางผู้ผลิตให้ถี่ถ้วน เพื่อให้สามารถออกแบบตำแหน่งการวางหัวจ่ายได้เหมาะสมกับลักษณะงานที่ต้องการ ทั้งนี้ ข้อมูลที่สำคัญอีกอย่างที่ควรทราบก่อนการออกแบบ คือลักษณะภูมิศาตร์ของพื้นที่ ว่ามีตำแหน่งสูงต่ำคร่าวๆเท่าใด เพราะจะมีผลต่อ Head ที่ตำแหน่งต่างๆในพื้นที่ และในกรณีที่ตัวปัมป์อยู่สูงกว่าพื้นที่ที่ต้องการจ่ายน้ำพอสมควร อาจต้องมีการติดตั้งวาล์วสูญญากาศที่ต้นทางของท่อ เพื่อป้องกันการเกิดสูญญากาศในท่อ ซึ่งอาจทำให้ท่อยุบตัวหลังจากที่ปัมป์หยุดทำงาน

ในส่วนของการเลือกท่อส่งนั้น จะมีหลักการเบื้องต้นดังนี้

• เลือกสเปคของแรงดันของท่อให้เหมาะสม เช่นในกรณีของท่อ PE ทางผู้ผลิตจะมีการแจ้งค่า Pressure nominal โดยจะระบุเป็น PN ของท่อ ตามด้วยตัวเลขแรงดันใช้งานในหน่วย bar เช่น PN6.3 หมายถึงท่อสำหรับใช้งานที่แรงดันปกติไม่เกิน 6.3 bar
• เลือกขนาดท่อให้ Head loss ที่จะเกิดขี้นในท่อไม่ส่งผลให้เกิดปัญหาการจ่ายน้ำที่ไม่ทั่วถึง เช่นในกรณีของ sprinkler ที่ได้กล่าวมาแล้ว sprinkler แต่ละตัวควรจะเห็นแรงดันต่างกันประมาณไม่เกิน 20% ของแรงดันใช้งาน
• เพื่อป้องกันความเสียหายของท่อส่งและการสูญเสียแรงดันที่มากเกินไป ควรออกแบบให้น้ำในท่อส่งมีอัตราเร็วของการไหลไม่เกิน 1.5 m/s

ในส่วนของการเลือกปัมป์น้ำนั้น ก่อนอื่น เราจำเป็นต้องคำนวณหา Head และอัตราไหลของน้ำที่ปัมป์ต้องจ่าย โดยในส่วนของอัตราไหลของน้ำนั้น จะคำนวณได้จากการรวมอัตราไหลของน้ำที่หัวจ่ายทุกหัวที่ต้องการเปิดใช้งานพร้อมกัน ส่วนค่า Head ที่ปัมป์จะต้องทำได้ จะประกอบไปด้วย^††

• ระยะความสูงของตัวปัมป์จากแหล่งน้ำ (suction lift)
• Head loss ที่เกิดที่อุปกรณ์ต้นทาง (control) เช่น อุปกรณ์กรองน้ำ มาตรวัดน้ำ
• Head loss ในท่อน้ำทั้งหมดจนถึงหัวจ่ายสุดท้ายของสาย
• Head ที่หัวจ่ายใช้ในการทำงาน
• ความแตกต่างของความสูงในพื้นที่เทียบกับตัวปัมป์ (อาจมีค่าเป็นลบได้ถ้าพื้นที่รดน้ำอยู่ต่ำกว่าตัวปัมป์)
• Head loss ที่ fittings และ valves ต่างๆ

สำหรับ Head loss ที่ fittings และ valves อาจคิดคร่าวๆได้ โดยคิดเป็น 10% ของ Head ที่ปัมป์ต้องจ่ายโดยยังไม่รวมความแตกต่างของความสูงของพื้นที่ (นั่นคือ 10% ของ (suction lift+Head loss ในอุปกรณ์ต้นทาง+Head loss ในท่อน้ำทั้งหมดจนถึงหัวจ่าย+Head ที่หัวจ่ายใช้ในการทำงาน))

หมายเหตุ จะเห็นได้ว่าเราไม่ได้รวมเทอมของการเปลี่ยนแปลงพลังงานจลน์ (v²/2g ใน Bernoulli equation) เข้าใน Head ที่ปัมป์ต้องจ่าย เนื่องจากค่านี้มักจะไม่สูง โดยเฉพาะถ้าเราควบคุมอัตราเร็วน้ำไม่ให้เกิน 1.5 m/s

นอกจากนี้ ในการติดตั้งปัมป์ หากมีการดูดน้ำขึ้นจากแหล่งน้ำ ก็ควรคำนึงถึงตำแหน่งปัมป์ว่าจะสามารถติดตั้งได้สูงแค่ไหนจากแหล่งน้ำ (ดูหัวข้อการเลือกปัมป์น้ำ) และควรมีการติดตั้งหัวกะโหลกที่มีวาล์วกันน้ำไหลย้อน (foot valve) ที่ปลายสายดูด เพื่อให้มีน้ำเลี้ยงอยู่ในสายดูดตลอดเวลาถึงแม้ว่าจะปิดปัมป์ ซึ่งจะช่วยให้ไม่ต้องล่อน้ำ (priming) ทุกครั้งก่อนที่จะใช้งาน ในส่วนของท่อส่งที่ออกจากปัมป์ก็ควรมีการติดตั้งวาล์วกันน้ำย้อนกลับ (check valve) ด้วยเช่นกัน เพื่อรักษาปัมป์ในกรณีที่มีแรงดันย้อนกลับจากระบบ

ตัวอย่างที่ 3: การออกแบบระบบน้ำ

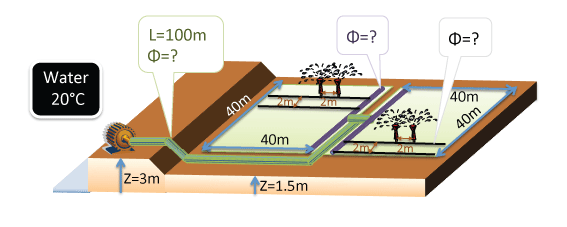
พิจารณาระบบน้ำด้านบน ซึ่งต้องการจ่ายน้ำเพื่อรดน้ำแปลงผัก 2 แปลง โดยจะรดน้ำทีละแปลง (ใช้การสับวาล์ว) ไม่รดพร้อมกัน แต่ละแปลงมีขนาด 40x40m² และอยู่ในระดับความสูงเดียวกันหมด โดยในแต่ละแปลง ต้องการรดน้ำโดยใช้ sprinkler โดยติดตั้งที่ทุกๆ 2x2m² โดย sprinkler ที่ใช้มีแรงดันใช้งานที่ประมาณ 2 bar จ่ายน้ำที่ 50l/hr ที่ 2 bar และมีค่า x ที่ประมาณ 0.5

ให้ใช้ J_Q,pipeของแผนภูมิตัวอย่าง A คำนวณหา

• a) ขนาดของท่อที่เหมาะสมสำหรับสายส่ง lateral แต่ละเส้น (ท่อสีดำในรูป)
• b) ขนาดของท่อที่เหมาะสมสำหรับสายส่งรอง (2nd) (ท่อสีม่วงในรูป)
• c) ขนาดของท่อที่เหมาะสมสำหรับสายส่งหลัก (1st) (ท่อสีเขียวในรูป)
• d) อัตราไหลและ Head ที่ปัมป์ต้องจ่าย

a) ออกแบบขนาดท่อส่ง lateral

จากรูป จะเห็นว่าในแต่ละสาย lateral จะมี sprinkler อยู่จำนวน N=40m/2m=20 ตัว ซึ่งเราสามารถหาค่า F ของ lateral ได้เป็น (โดยคิดว่าหัวจ่ายแรกอยู่ที่ระยะ 1 เมตรจากสายส่งรอง และใช้ m=2)

$$ F_{lat}=\frac{1}{2+1}+\frac{1}{2 \times 20}+\frac{\sqrt{2-1}}{6 \times 20^2}=0.359$$

จากหัวข้อที่แล้ว หากเราต้องการให้ sprinkler ตัวแรกและตัวสุดท้ายของสายมีอัตราจ่ายน้ำต่างกันไม่เกิน 10% เราต้องออกแบบให้หัวจ่ายเห็นแรงดันต่างกันไม่เกิน 20% นั่นคือ แรงดันสูญเสียในสาย lateral จะต้องไม่เกิน 0.2x2bar=0.4bar หรือ คิดเป็น Head loss ไม่เกิน 0.4/0.098=~4m ซึ่งถ้าเราใช้สูตร ของ manifold จะพบว่า

$$ ΔH_{lat,pipe}={ΔH_{lat,manifold} \over F_{lat}}={4 \over 0.359}=11.14m $$

นั่นคือ เราต้องเลือกสายที่สามารถจ่ายน้ำได้ที่

$$Q_{total,lat}= Q_{sprinkler} \times N_{sprinkler}=50 \times 20=1000l/hr$$ $$=\frac{1000}{3600}l/s=0.278l/s$$

และค่า J_Q,pipe ต้องไม่เกิน

$$J_{Q,pipe,lat} \le {ΔH_{lat,pipe} \over L_{lat}}=\frac{11.14}{40}=0.279$$

ซึ่งหากเราตรวจสอบดูจากแผนภูมิ J_Q,pipe ตัวอย่าง A จะเห็นได้ว่าที่ Q=0.278l/s นั้น ท่อ 16mm/PN12.5 จะให้ค่า J_Q,pipe อยู่ที่ 50/100=0.5 ซึ่งมากเกินไป ดังนั้นเราต้องเลือกขนาดท่อที่ใหญ่ขี้นคือ ท่อ 20mm/PN12.5 (ไม่จำเป็นต้องเลือก PN16 เพราะแรงดันใช้งานของเราเพียงประมาณ 2 bar) ซึ่งจะให้ค่า J_Q,pipe อยู่ที่ 16/100=0.16 ทั้งนี้ การเลือกท่อขนาดใหญ่ขึ้นก็เป็นสิ่งจำเป็นอยู่แล้ว เนื่องจากเราจำเป็นต้องเผื่อแรงดันที่จะต้องตกเพิ่มเติมในสายส่งรอง ซึ่งอาจส่งผลให้ Head loss เกิน 20% ได้

ทั้งนี้เราควรต้องเช็คด้วยว่าอัตราเร็วของน้ำในท่อจะเกิน 1.5m/s หรือไม่ ซึ่งจะเห็นได้ทันทีจากในแผนภูมิ J_Q,pipe ตัวอย่าง A ว่าไม่เกิน จึงสามารถนำมาใช้งานได้ โดยเมื่อเราเลือกขนาดท่อที่ต้องการได้แล้ว เราจะสามารถคำนวณหา Head loss ในสาย lateral ได้ ดังนี้

$$ ΔH_{lat,manifold} = 0.359 \times 0.16\times 40=2.3m $$

b) ออกแบบขนาดท่อส่งรอง

สำหรับสายส่งรองนั้น เราก็สามารถใช้หลักการเดียวกันกับในข้อ a) ได้ อย่างไรก็ดี ในที่นี้ เราจะเห็นได้ว่าข้อกำหนดที่จะให้ Head loss ของ sprinkler ทุกๆตัวในระบบต่างกันไม่เกิน 4 m จะเหลือเป็น 4-2.3=1.7m (เนื่องจากเราทราบแล้วว่าสาย lateral มี Head loss จากต้นถึงปลายสายเป็น 2.3m อยู่แล้ว) ทั้งนี้ ในการคำนวณหาขนาดสายส่งรองนี้ เราสามารถคำนวณเพียง 1 แขนของสายส่ง จาก 4 แขน (ดูรูป) ซึ่งใน 1 แขน จะมีทางออกน้ำอยู่ N=1/2x40m/2m=10 จุด ซึ่งถ้าเราใช้ m ที่ 2.0 จะได้ว่า

$$ F_{2nd}=\frac{1}{2+1}+\frac{1}{2 \times 10}+\frac{\sqrt{2-1}}{6 \times 10^2}=0.385$$

และถ้าต้องการให้ Head loss ไม่เกิน 1.7m จะพบว่า

$$ ΔH_{2nd,pipe} = {ΔH_{2nd,manifold} \over F_{2nd}}={1.7 \over 0.385}=4.42m $$

นั่นคือ เราต้องเลือกสายที่สามารถจ่ายน้ำได้ที่

$$Q_{total,2nd}= Q_{lat} \times N_{lat}=1000 \times 10=10000l/hr$$ $$=\frac{10000}{3600}l/s=2.78l/s$$

และค่า J_Q,pipe ต้องไม่เกิน

$$J_{Q,pipe,2nd} \le {ΔH_{2nd,pipe} \over L_{2nd}}=\frac{4.42}{20}=0.221$$

ซึ่งหากเราตรวจสอบดูจากแผนภูมิ J_Q,pipe ตัวอย่าง A จะเห็นได้ว่าที่ Q=2.78l/s นั้น ท่อที่ให้ค่า J_Q,pipe ต่ำกว่า 0.221 พอดี จะเป็นท่อ 40mm/PN6.3 อย่างไรก็ดี จะเห็นจากแผนภูมิว่า หากเลือก ท่อ 40mm/PN6.3 อัตราเร็วของน้ำจะสูงกว่า 2.5m/s (โดยเฉพาะในส่วนที่ใกล้ต้นทาง เพราะยังไม่มีการจ่ายน้ำออกไปแต่ละ lateral) ซึ่งจะมากกว่าเกณฑ์ 1.5m/s ที่ได้กล่าวมาแล้ว ดังนั้น เราควรเลือกท่อที่ให้อัตราเร็วน้ำไม่เกิน 1.5m/s ที่ Q=2.78L/s ซึ่งจากแผนภูมิ จะพบว่าเราควรจะเลือกท่อ 63mm/PN6.3 ซึ่งจะให้ค่า J_Q,pipe อยู่ที่ประมาณ 2.3m/100m

หลังจากที่เลือกขนาดท่อที่ต้องการแล้ว เราจะสามารถคำนวณหา Head loss ในสายส่งรองได้ ดังนี้

$$ ΔH_{2nd,manifold} = 0.385 \times 0.023 \times 20=0.177m $$

โดย ณ. เวลานี้ เราจะสามารถคำนวณหาแรงดันต่างระหว่าง sprinkler ตัวที่อยู่ใกล้ต้นทางที่สุดและตัวที่อยู่ห่างที่สุดได้เป็น

$$ΔH_{sprinkler,max}=ΔH_{2nd,manifold}+ΔH_{lat,manifold}=0.177+2.3$$ $$=2.48m$$

หรือคิดเป็น bar จะได้

$$ΔP_{sprinkler,max}=2.48 \times 0.098=0.24bar$$

ซึ่งจะยังคงน้อยกว่า 20% ของ 2 bar ตามที่ต้องการอยู่

c) ออกแบบขนาดท่อส่งหลัก

ในกรณีของสายส่งหลักนั้น เราไม่จำเป็นต้องคิดถึงเรื่องแรงดันที่จะทำให้ sprinkler จ่ายน้ำไม่เท่ากัน เพียงแต่พิจารณาในเรื่องแรงดันตกที่เรารับได้ และในอัตราเร็วน้ำที่ไม่เกิน 1.5 m/s ซึ่งในกรณีนี้ อัตราไหลของน้ำที่สายส่งหลักจะต้องจ่ายเพื่อรดหนึ่งแปลงผักจะเท่ากับ

$$Q_{total,1st}= 2 \times 10000l/hr=20m^3/hr=2 \times 2.78l/s=5.56l/s$$

ซึ่งเมื่อตรวจสอบจากแผนภูมิ J_Q,pipe ตัวอย่าง A จะพบว่าที่ 5.56l/s ท่อขนาด 75mm/PN6.3 จะให้อัตราเร็วน้ำที่สูงกว่า 1.5m/s เล็กน้อย ดังนั้นจึงควรเลือก ท่อขนาดถัดไป คือ 90mm/PN6.3 ซึ่งมิได้แสดงในแผนภูมิตัวอย่าง A โดยเราสามารถดูที่แผนภูมิตัวอย่าง B ซึ่งจะได้ว่าที่ Q=5.56l/s จะให้ค่า J_Q,pipe ประมาณ 13m/1000m ดังนั้นเราจะคำนวณหา Head loss ในสายส่งหลักนี้ได้เป็น

$$ ΔH_{1st,pipe} = J_{Q,90mmPN6.3} \times L_{1st}= \frac{13}{1000} \times 100=1.3m$$

หรือคิดเป็น bar จะได้

$$ΔP_{1st,pipe}=1.3 \times 0.098=0.127bar$$

d) คำนวณหาอัตราไหลและ Head ที่ปัมป์ต้องจ่าย

Head ที่ปัมป์ต้องทำให้ได้ สามารถคำนวณได้ดังนี้ (โดย Head loss ที่เกิดจากอุปกรณ์ต้นทาง เช่นเครื่องกรอง จำเป็นต้องคำนวณตามข้อมูลของผู้ผลิตนั้นๆ โดยในที่นี้ จะใช้ค่า 7m)

$$Head_{suction} = 3m$$ $$ΔHead_{control} = 7m$$ $$ΔHead_{1st,pipe} = 1.3m$$ $$ΔHead_{2nd,manifold} = 0.18m$$ $$ΔHead_{lateral,manifold} = 2.3m$$ $$Head_{sprinkler} = {2 \over 0.098} =20.41m$$

ซึ่งจะรวมได้เป็น

$$Head_{subtotal}=3+7+1.3+0.18+2.3+20.41=34.19m$$ $$ΔHead_{fittings}={10 \over 100} \times 34.19 =3.42m$$ $$ΔZ=Z_2-Z_1=1.5-3.0=-1.5m$$

เพราะฉะนั้น Head ที่ปัมป์ต้องทำให้ได้ คือ

$$Head_{pump}=34.19+3.42-1.5=36.1m$$

หรือคิดเป็น bar ได้

$$P_{pump}=36.1 \times 0.098 =3.54 bar$$

ที่

$$Q_{pump}=20 m^{3}/hr $$

ในการเลือกปัมป์น้ำ มีแผนภูมิ 4 อย่างที่ควรต้องรู้จักและทำความเข้าใจเสียก่อน ซึ่งแผนภูมิทั้งสี่นี้แสดงค่า 4 อย่างที่อัตราไหลต่างๆ ดังแสดงในรูปตัวอย่างข้างล่างนี้ (Source: Pedrollo 2CP Series-Characteristic curves and performance data)

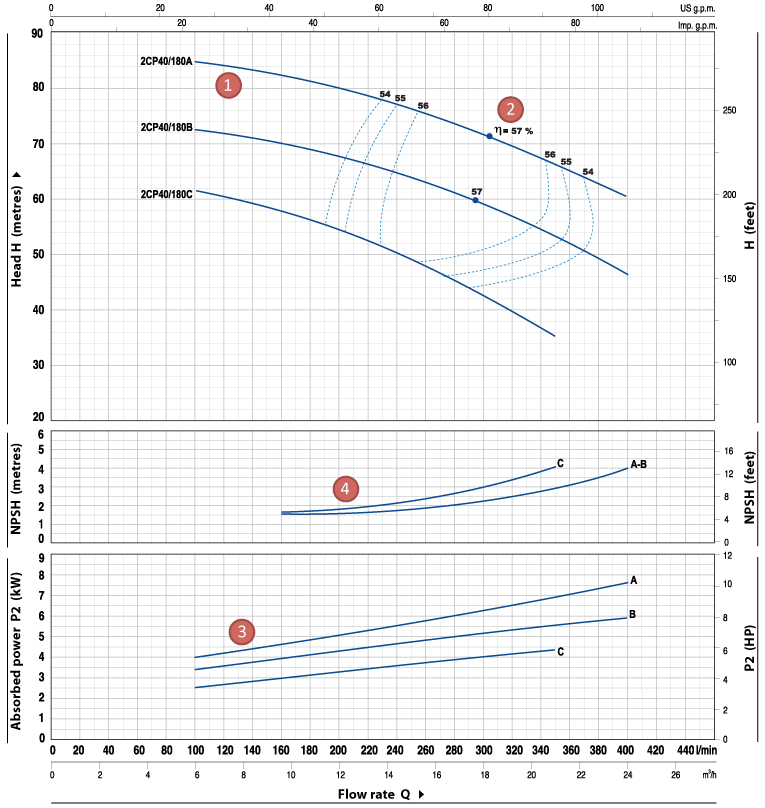
1.แผนภูมิ Q-H (Head vs. Flow rate)

เป็นแผนภูมิหลักที่สำคัญที่สุดในการเลือกปัมป์ โดยจะแสดง Head ที่อัตราไหลต่างๆที่ปัมป์ทำได้ โดยลักษณะสำคัญของแผนภูมินี้ คือ Head หรือแรงดันสูดสุดที่ปัมป์ทำได้จะเกิดขี้นที่อัตราไหลเป็นศูนย์ (เช่นในขณะที่ปัมป์ทำงาน แต่ปิดวาล์วทุกวาล์วในระบบ) และ Head ที่ปัมป์ทำได้จะลดลงตามปริมาณน้ำที่ปัมป์์ต้องจ่ายเพิ่มขี้น

ดังที่ได้กล่าวมาแล้ว ก่อนที่จะทำการเลือกปัมป์เราจำเป็นต้องทราบก่อนว่าระบบน้ำของเราต้องการ Head และอัตราไหลที่เท่าไหร่ ที่ปัมป์จะต้องจ่าย (ดูจากหัวข้อที่แล้ว) แล้วจึงเลือกปัมป์ที่สามารถตอบสนองจุดทำงานนั้นได้ ทั้งนี้ ควรที่จะเลือกจุดทำงานที่ใกล้กับจุดที่มีประสิทธิภาพสูงสุดของปัมป์ ซึ่งสามารถดูได้จากแผนภูมิถัดไป

2.แผนภูมิ Q-η (Efficiency vs. Flow rate)

โดยทั่วไปหากมิได้ระบุชัดเจนเป็นอย่างอื่น ประสิทธิภาพนี้คือประสิทธิภาพของตัวปัมป์ในส่วนที่ทำให้เกิดแรงดันน้ำ (ซึ่งยังมิได้รวมส่วนของประสิทธิภาพของมอเตอร์) ซึ่งคำนวณได้จาก

โดย

η_p คือประสิทธิภาพของปัมป์น้ำ

P_H คือกำลังที่ปัมป์ส่งให้น้ำ (W)

P₂ คือกำลังขาเข้าที่เพลาปัมป์ (W)

ρ คือ ความหนาแน่นของน้ำ หน่วย (Kg/m³)

g คือ อัตราเร่งเนื่องจากแรงโน้มถ่วงของโลก (9.81 m²/s)

Q คืออัตราไหลของน้ำ (m³/s)

H คือ Head (m)

ดังที่ได้กล่าวแล้ว การเลือกปัมป์ควรเลือกให้จุดทำงานอยู่ใกล้จุดที่มีประสิทธิภาพสูงสุด แต่ในขณะเดียวกันก็ควรมีการเผื่อในกรณีที่ต้องมีการจ่ายน้ำที่อัตราสูงขี้นบ้างเช่นกัน

3.แผนภูมิ Q-P₂ (Power into pump shaft vs. Flow rate)

แผนภูมินี้แสดงค่าสุทธิของกำลังที่ต้องส่งให้เพลาของปัมป์ เพื่อให้ได้อัตราไหลและแรงดันตามที่แผนภูมิ Q-H แสดง

4.แผนภูมิ Q-NPSH (Net Positive Suction Head vs. Flow rate)

NPSH คือ ค่าแรงดัน(สุทธิ)ที่ต่ำที่สุดที่ของเหลวต้องมี ณ.ขาเข้าของปัมป์ เพื่อไม่ให้เกิดโพรงอากาศในตัวปัมป์ขณะที่ปัมป์ทำงาน โดยค่า NPSH นี้ จะสูงขี้นเมื่อปัมป์ต้องจ่ายน้ำที่อัตราสูงขี้น

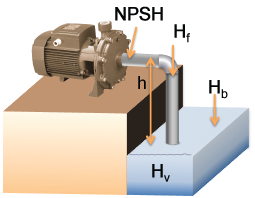
ค่า NPSH นี้ จะเป็นตัวกำหนดว่า เราจะสามารถติดตั้งปัมป์ที่ความสูงที่สุดเท่าไหร่จากผิวน้ำของแหล่งน้ำที่ปัมป์ต้องดูดขี้นมา โดยจะคำนวณได้จาก

h_max คือ ความสูงที่มากที่สุดที่ตัวปัมป์จะอยู่สูงจากผิวน้ำของแหล่งน้ำได้

H_b คือความดันบรรยากาศที่ผิวน้ำของแหล่งน้ำ ซึ่งจะขี้นอยู่กับความสูงของพื้นที่เทียบกับระดับน้ำทะเล

H_f คือ Head Loss ในสายดูด

NPSH_operating คือ ค่า NPSH ที่อ่านได้จากแผนภูมิ โดยควรอ่านที่อัตราไหลสูงสุดที่ต้องการใช้งาน

H_v คือ ความดันไอของน้ำ (water vapour pressure) (ดูค่าที่อุณภูมิต่างๆได้ที่ตารางล่างสุดในหน้าเวปนี้)

H_s คือ Safety factor ของ Head ซึ่งโดยปกติ จะตั้งที่ 0.5-1m เว้นแต่ในของเหลวมีก๊าซอยู่

ตารางแสดงค่าคุณสมบัติของน้ำที่อุณหภูมิต่างๆ

^†Source: J.E. Christiansen,"Irrigation by Sprinkling"--LINK--
^††Source: A.P. Savva and K.Frenken,"Irrigation Manual, Volume IV" --LINK--